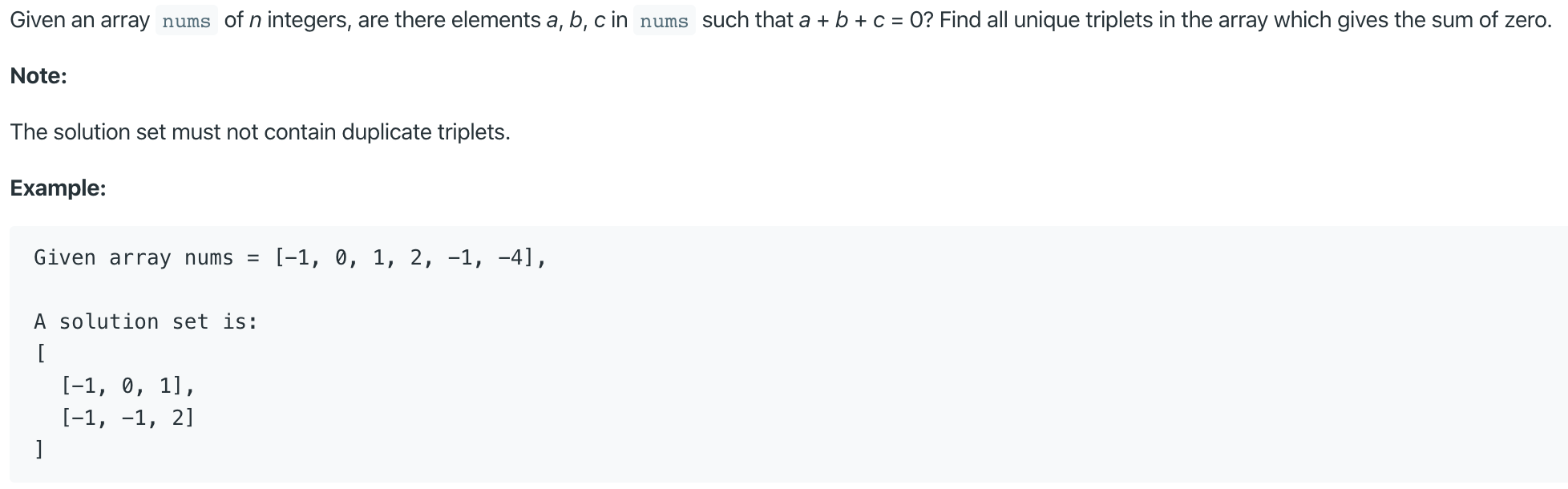
Three Sum

Solution

The brute force solution doesn't sort and takes 3 nested for loops for cubic time.

Sorting($O(n \log n)$) was not a good practice in linear time two sum but should be used in this squared time problem.

Vanilla Two Pointers

Sort and then use two pointers to search for satisfied result. Caveat is to look out for duplicates.

Complexity

time: $O(n^2)$
space: $O(n^2)$

def threeSum(self, nums: List[int]) -> List[List[int]]:
    res = []
    nums.sort()
    for i in range(len(nums)-2):
        # no need to continue searching b/c nums is sorted
        if nums[i] > 0:
            break
        # i>0 s.t. i-1>=0
        # continue if `curr == prev` to eliminate duplicates on smallest elt
        if i > 0 and nums[i] == nums[i-1]:
            continue
        target = -nums[i]
        left = i + 1
        right = len(nums) - 1

        while left < right:
            if nums[left] + nums[right] == target:
                res.append([nums[left], nums[i], nums[right]])
                # if the current left/right is the same w/ the next, a duplicate would be returned
                while left < right and nums[left] == nums[left+1]:
                    left += 1
                while left < right and nums[right] == nums[right-1]:
                    right -= 1
                # update left/right after eliminating duplicates
                left += 1
                right -= 1
            elif nums[left] + nums[right] < target:
                left += 1
            else:
                right -= 1
    return res

Return a Set

Also sort and then use two pointers, but the difference is returning a set rather than list.

To eliminate duplicates, use tuple rather than list for HashSet res.

Complexity

time: $O(n^2)$
space: $O(n^2)$

def threeSum(self, nums: List[int]) -> List[List[int]]:
    res = set()
    n = len(nums)
    nums.sort()

    for i in range(n-2):
        target = -nums[i]
        left = i + 1
        right = n - 1
        while left < right:
            # speed up a bit
            if nums[i] > 0:
                break
            if nums[left] + nums[right] == target:
                res.add((nums[i], nums[left], nums[right]))
                left += 1
                right -= 1
            elif nums[left] + nums[right] < target:
                left += 1
            else:
                right -= 1
    return res