Longest Palindromic Substring

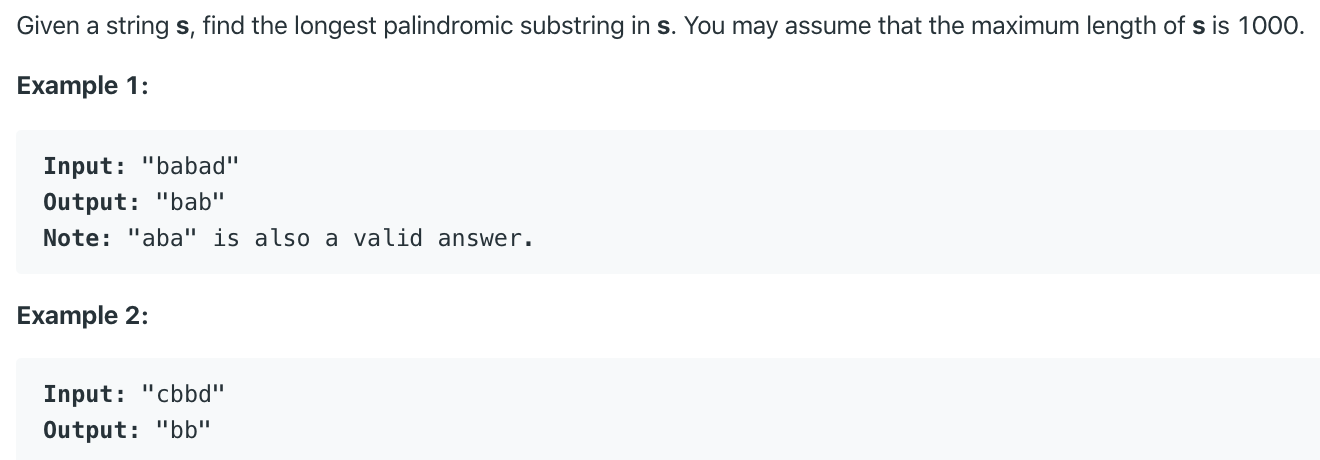
Please don't confuse this problem w/ the longest common substring (opens new window) or longest common subsequence.

Solution

Let $n$ be the length of string s.

Brute Force

Complexity

time: $O(n^3)$
space: $O(1)$

The brute force solution can be further optimized to expand around center by expanding one char at a time in the left and right direction under odd and even cases.

def longestPalindrome(self, s: str) -> str:
    if not s: return ""
    res = s[0]
    for i in range(len(s)):
        for j in range(i + 1, len(s)+1):
            if self.isPalindrome(s[i:j]) and j - i + 1 > len(res):
                res = s[i:j]
    return res

def isPalindrome(self, s: str) -> bool:
    i = 0
    j = len(s) - 1
    while i<=j:
        if s[i] == s[j]:
            i += 1
            j -= 1
        else:
            return False
    return True

DP

Let dp[i][j] be true if s[i:j+1] is a palindrome and false otherwise.

The state transition is:
dp[i][j] = s[i] == s[j] and dp[i+1][j-1]

The base cases are:
dp[i][i] = True
dp[i][i+1] = s[i] == s[i+1]

Both the state transition and base cases can be combined into dp[i][j] = s[i] == s[j] and (j - i < 3 or dp[i+1][j-1]).

Complexity

time: $O(n^2)$
space: $O(n^2)$

def longestPalindrome(self, s: str) -> str:
    n = len(s)
    dp = [[False for _ in range(n)] for _ in range(n)]
    res = ""
    for i in reversed(range(n)):
        for j in range(i, n):
            dp[i][j] = s[i] == s[j] and (j - i < 3 or dp[i+1][j-1])
            if dp[i][j] and j - i + 1 > len(res):
                res = s[i:j+1]
    return res

Expand around Center

A palindrome mirrors around its center. The center for odd-length palindrome is the central character. The center for even-length palindrome is between the central 2 characters. There are $2n - 1$ such centers and expanding around each center takes linear time.

Complexity

time: $O(n^2)$
space: $O(1)$

def longestPalindrome(self, s: str) -> str:
    n = len(s)
    res = ""
    for i in range(n):
        # odd-length longest palindrome
        odd = self.expandAroundCenter(s, i, i)
        if len(odd) > len(res):
            res = odd
        # even-length longest palindrome
        even = self.expandAroundCenter(s, i, i+1)
        if len(even) > len(res):
            res = even
    return res

def expandAroundCenter(self, s: str, l, r):
    while l >= 0 and r < len(s) and s[l] == s[r]:
        l -= 1
        r += 1
    return s[l+1:r]

Manacher's Algorithm

This algorithm includes some smart improvements on Expand around Center.

See more at windliang's post (opens new window).

Complexity

time: $O(n)$ (each element is traversed at most twice)
space: $O(n)$

def longestPalindrome(self, s: str) -> str:
    # e.g. s = "abba", T = "^#a#b#b#a#$" (odd length)
    # ^ and $ signs are sentinels appended to each end to avoid bounds checking
    T = '#'.join('^{}$'.format(s))
    n = len(T)
    P = [0 for _ in range(n)]
    C = R = 0
    max_center = 0
    max_len = -1

    for i in range(1, n-1):
        # w/i right boundary, can save time by copying mirror length
        if i < R:
            mirror = 2*C - i
            P[i] = min(R-i, P[mirror])

        # expand around i
        while T[i+(1+P[i])] == T[i-(1+P[i])]:
            P[i] += 1

        # update the center & right
        if i + P[i] > R:
            C = i
            R = i + P[i]

        # update the best result so far
        if P[i] > max_len:
            max_center = i
            max_len = P[i]

    start, end = (max_center-max_len)//2, (max_center+max_len)//2
    return s[start: end]