Spiral Matrix

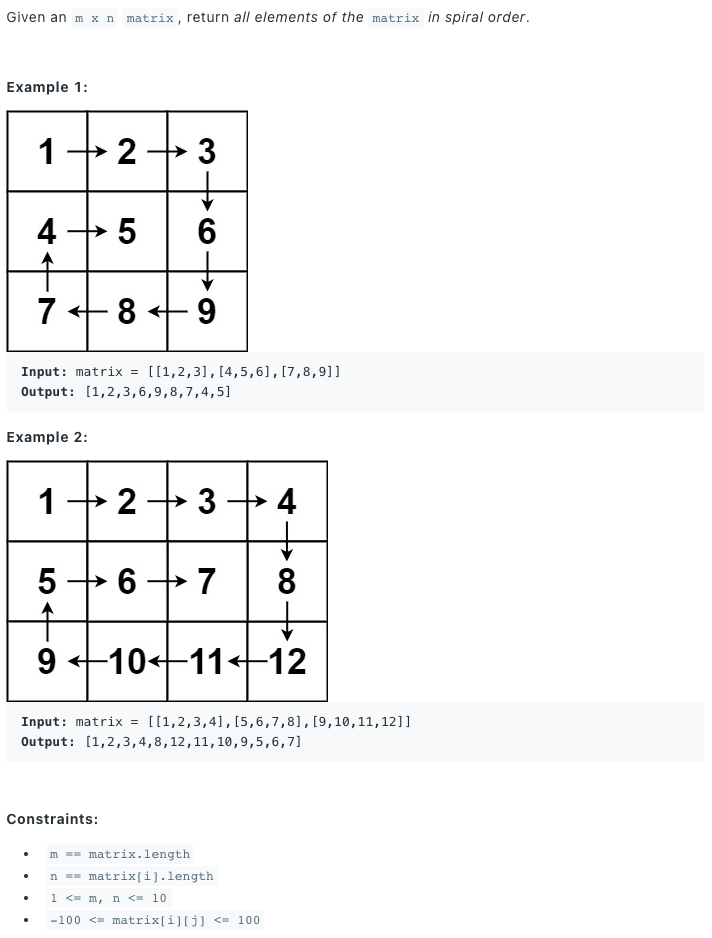
Solution

Let $N$ be the number of total elements in the matrix.

Simulation

Need seen and bounds checking to decide if next move needs to change direction.

Complexity

time: $O(N)$
space: $O(N)$

def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
    res = []
    if not matrix: return res
    R, C = len(matrix), len(matrix[0])
    seen = [[False for _ in range(C)] for _ in range(R)]
    r = c = di = 0
    dr = [0, 1, 0, -1]
    dc = [1, 0, -1, 0]

    for _ in range(R * C):
        res.append(matrix[r][c])
        seen[r][c] = True
        nr, nc = r+dr[di], c+dc[di]
        if 0 <= nr < R and 0 <= nc < C and not seen[nr][nc]:
            r, c = nr, nc
        else:
            di = (di + 1) % 4
            r, c = r+dr[di], c+dc[di]
    return res

Loop Inward

def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
    res = []
    if not matrix: return res
    R, C = len(matrix), len(matrix[0])
    r1 = 0
    r2 = R - 1
    c1 = 0
    c2 = C - 1
    while r1 <= r2 and c1 <= c2:
        # top: c from c1 ... c2
        for c in range(c1, c2+1):
            res.append(matrix[r1][c])
        # right: r from r1+1 ... r2
        for r in range(r1+1, r2+1):
            res.append(matrix[r][c2])
        if r1<r2 and c1<c2:
            # bottom: c from c2-1 ... c1+1
            for c in range(c2-1, c1, -1):
                res.append(matrix[r2][c])
            # left: r from r2 ... r1+1
            for r in range(r2, r1, -1):
                res.append(matrix[r][c1])
        r1 += 1
        c1 += 1
        r2 -= 1
        c2 -= 1
    return res