Sliding Puzzle II

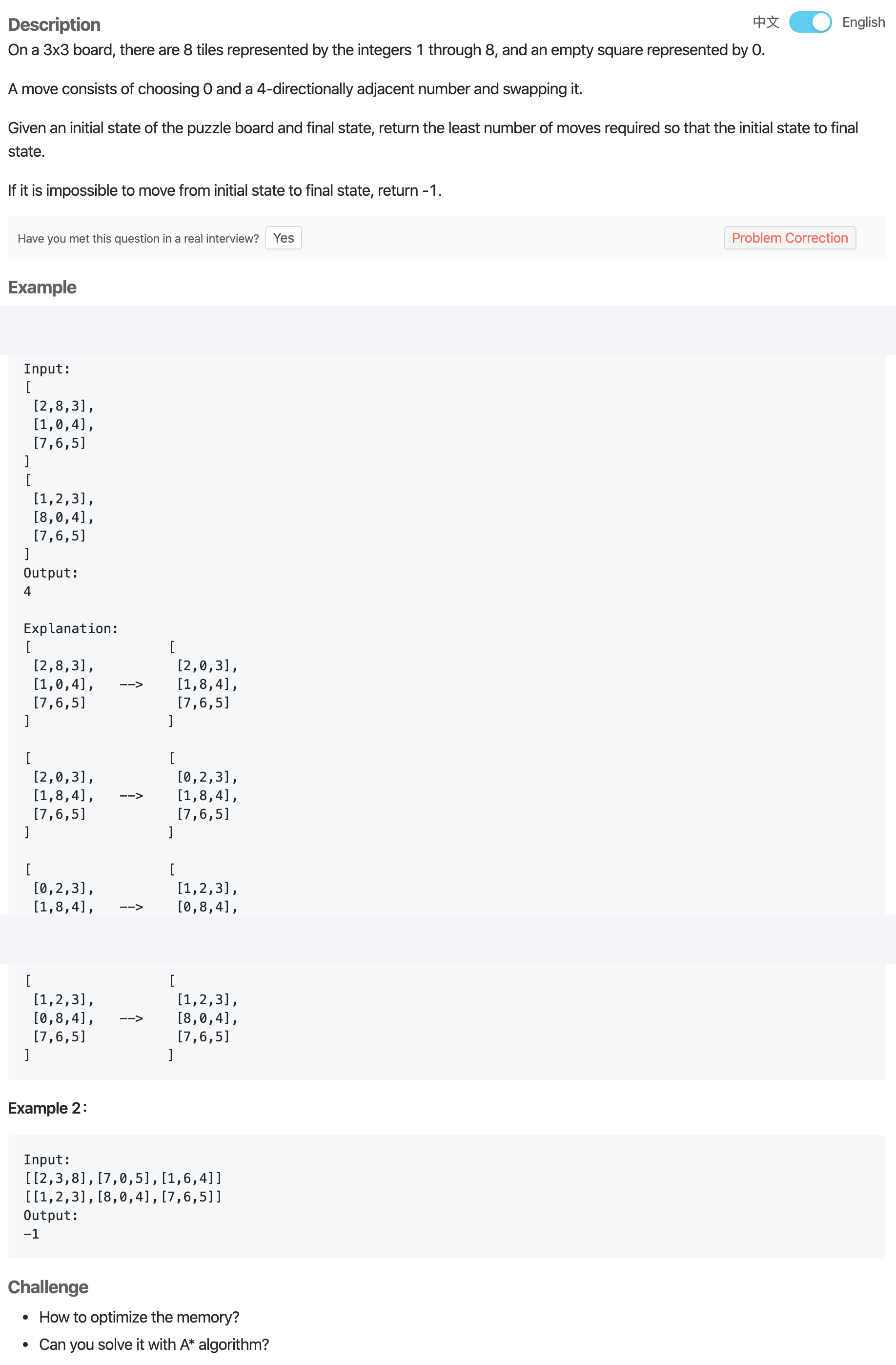
Input & Output

@param init_state: the initial state of chessboard
@param final_state: the final state of chessboard
@return: return an integer, denote the number of minimum moving

Solution

Let $n$ be the number of rows and $m$ be the number of columns.

See the previous easier problem for complexity analysis and A* algorithm solution.

Layered BFS

Note:

1. getNext helps find the neighbor nodes (states are like nodes in implicit graph)
2. matrixToString converts state from matrix to string

DIRECTIONS = [(-1, 0), (1, 0), (0, -1), (0, 1)]
def minMoveStep(self, init_state, final_state):
    init_state_str = self.matrixToString(init_state)
    final_state_str = self.matrixToString(final_state)
    queue = [init_state_str]
    vis = set()
    res = 0
    while queue:
        for _ in range(len(queue)):
            state = queue.pop(0)
            if state == final_state_str:
                return res
            for next_state in self.getNext(state):
                if next_state not in vis:
                    vis.add(next_state)
                    queue.append(next_state)
        res += 1
    return -1

def matrixToString(self, state_mat):
    """
    @param state_mat: 3 by 3 state matrix
    @return: state string of 9 chars
    """
    state_str = ''
    for i in range(3):
        for j in range(3):
            state_str += str(state_mat[i][j])
    return state_str

def getNext(self, state):
    """
    @param state: the current state of board
    @return: a list of next states
    """
    next_states = []
    pos = state.find('0')
    x, y = divmod(pos, 3)

    for dx, dy in DIRECTIONS:
        nx, ny = x + dx, y + dy
        if not 0<=nx<3 or not 0<=ny<3:
            continue
        npos = 3*nx + ny
        mn, mx = min(npos, pos), max(npos, pos)
        nstate = state[0:mn] + state[mx] + state[mn + 1:mx] + state[mn] + state[mx + 1:]
        next_states.append(nstate)
    return next_states