Franklin

Unique Paths

ArrayDP
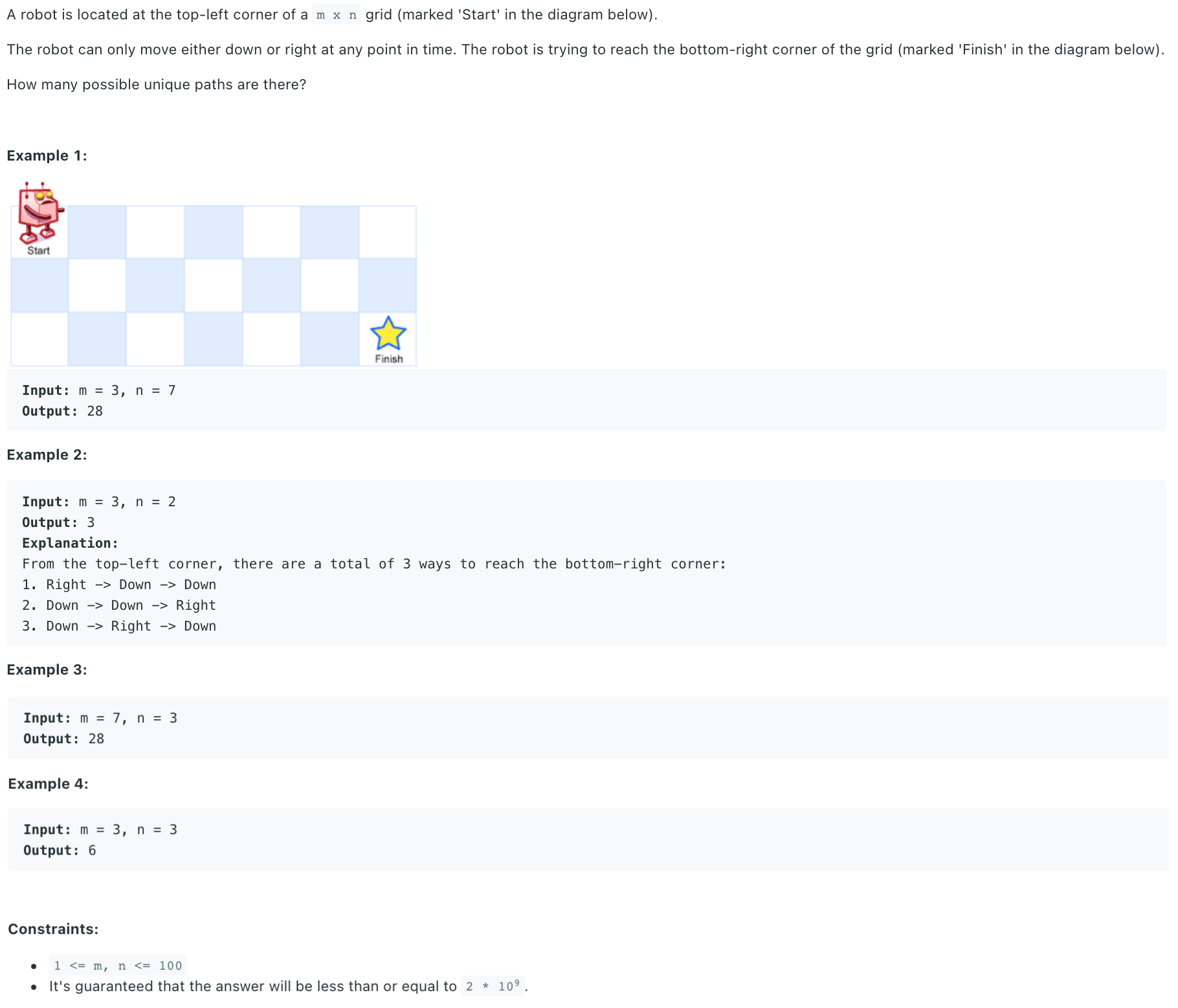
https://leetcode.com/problems/unique-paths

# Solution

We could exchange m and n s.t. m≤nm \leq n.

# DP

The state transition is: dp[i][j]=dp[i−1][j]+dp[i][j−1]dp[i][j] = dp[i-1][j] + dp[i][j-1]

The base cases are dp[0][j] and dp[i][0], which have by default only 11 path.

# Squared Space

Complexity

time: O(mn)O(mn)
space: O(mn)O(mn)

def uniquePaths(self, m: int, n: int) -> int:
    dp = [[0 for _ in range(n)] for _ in range(m)]
    for j in range(n):
        dp[0][j] = 1
    for i in range(1, m):
        dp[i][0] = 1
    for i in range(1, m):
        for j in range(1, n):
            dp[i][j] = dp[i-1][j] + dp[i][j-1]
    return dp[-1][-1]
1
2
3
4
5
6
7
8
9
10

# Linear Space

Complexity

time: O(mn)O(mn)
space: O(min⁡(m,n))O(\min(m, n))

def uniquePaths(self, m: int, n: int) -> int:
    if m > n: m, n = n, m
    dp = [[0 for _ in range(2)] for _ in range(m)]
    for i in range(m):
        dp[i][0] = 1
    dp[0][1] = 1
    for j in range(1, n):
        for i in range(1, m):
            dp[i][j%2] = dp[i-1][j%2] + dp[i][(j-1)%2]
    return dp[-1][(n-1)%2]
1
2
3
4
5
6
7
8
9
10

# Math

There are in total m−1+n−1=m+n−2m-1 + n-1 = m+n-2 moves, in which m−1m-1 moves are going down and n−1n-1 moves are going right. The number of unique paths is thus equal to m+n−2m+n-2 choose m−1m-1.

(m+n−2m−1)=(m+n−2)!(m−1)!(n−1)!=(m+n−2)(m+n−3)⋯n(m−1)!\binom{m+n-2}{m-1} = \frac{(m+n-2)!}{(m-1)!(n-1)!} = \frac{(m+n-2)(m+n-3) \cdots n}{(m-1)!}

Complexity

time: O(min⁡(m,n))O(\min(m, n))
space: O(1)O(1)

# 1-liner Cheating

from math import comb
def uniquePaths(self, m: int, n: int) -> int:
    return comb(m+n-2, m-1)
1
2
3

# Calculate by Formula

from math import comb
def uniquePaths(self, m: int, n: int) -> int:
    if m > n: m, n = n, m
    res = 1
    j = n
    for i in range(1, m):
        res *= j / i
        j += 1
    return round(res)
1
2
3
4
5
6
7
8
9

Valid Parenthesis