Longest Consecutive Sequence

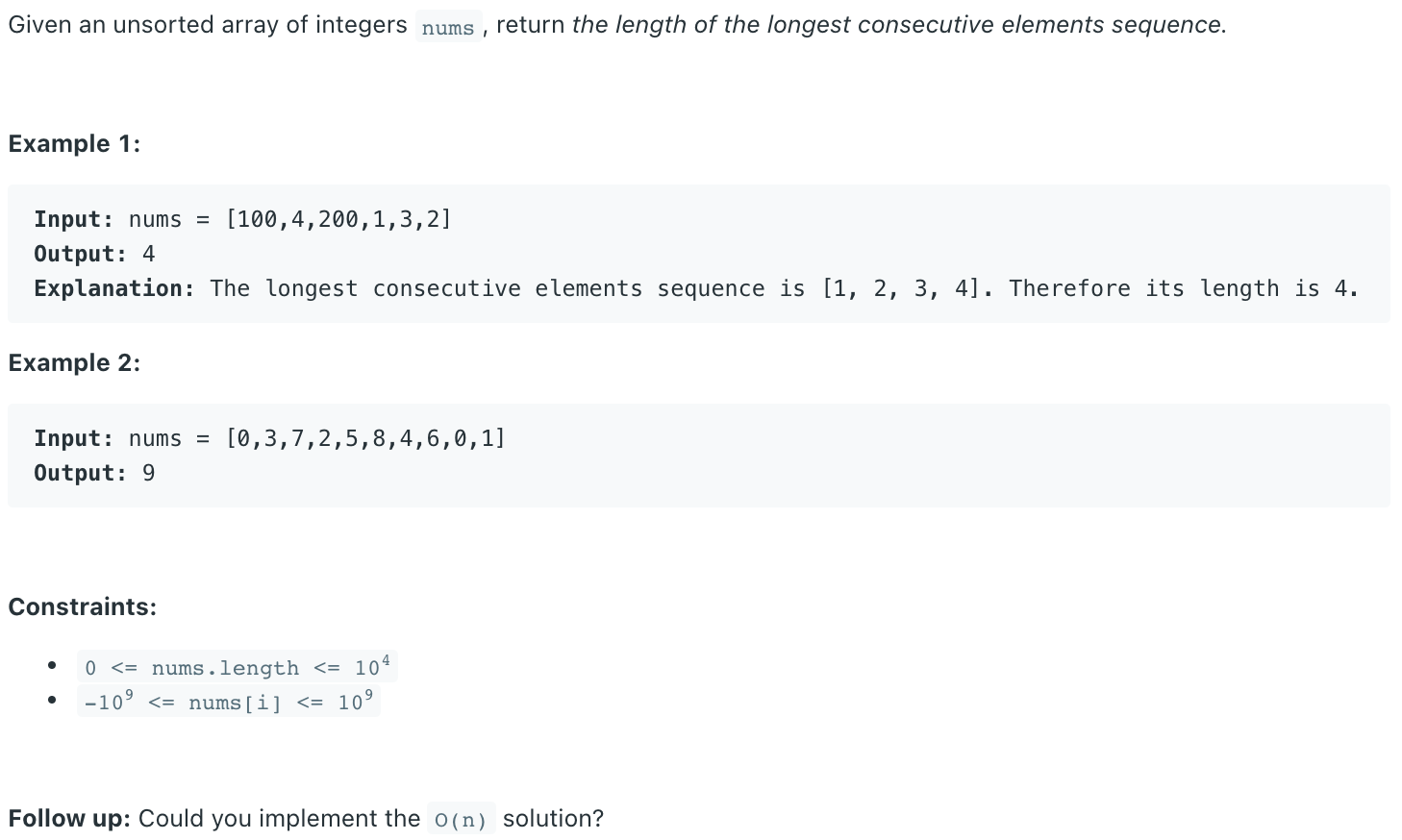
Solution

Let $n$ be the length of the array nums.

The brute force $O(n^3)$ solution is omitted.

Sort

Complexity

time: $O(n \log n)$
space: $O(1)$ (sort is in place)

def longestConsecutive(self, nums: List[int]) -> int:
    if not nums: return 0
    n = len(nums)
    curr_seq = 1
    res = 1
    # sort the sequence in place
    nums.sort()

    for i in range(1, n):
        # eliminate duplicates
        if nums[i] != nums[i-1]:
            # sequence is continued
            if nums[i] == nums[i-1]+1:
                curr_seq += 1
            # start a new sequence
            else:
                res = max(res, curr_seq)
                curr_seq = 1

    return max(res, curr_seq)

Follow up

Could you implement the $O(n)$ solution?

HashSet

Complexity

time: $O(n)$
space: $O(n)$

def longestConsecutive(self, nums: List[int]) -> int:
    res = 0
    hashset = set(nums)

    for num in nums:
        # find the start of sequence
        if num - 1 not in hashset:
            curr_num = num
            curr_seq = 1
            # sequence can be continued
            while curr_num + 1 in hashset:
                curr_num += 1
                curr_seq += 1
            # update longest consecutive sequence seen so far
            res = max(res, curr_seq)

    return res

Union Find (REDO)

Complexity

time: $O(n)$
space: $O(n)$

See more in Interview Algorithms and this LeetCode post (opens new window).

class Node:
    def __init__(self, val):
        self.val = val
        self.parent = self
        self.size = 1

class UnionFind:
    def find(self, node):
        if node.parent != node:
            node.parent = self.find(node.parent)
        return node.parent

    def union(self, node1, node2):
        parent_1 = self.find(node1)
        parent_2 = self.find(node2)
        if parent_1 != parent_2:
            parent_2.parent = parent_1
            parent_1.size += parent_2.size
        return parent_1.size

class Solution:
    def longestConsecutive(self, nums: List[int]) -> int:
        uf = UnionFind()
        nodes = {}
        max_size = 0
        for num in nums:
            if num not in nodes:
                node = Node(num)
                nodes[num] = node
                size = 1
                if num + 1 in nodes:
                    size = uf.union(node, nodes[num+1])
                if num - 1 in nodes:
                    size = uf.union(node, nodes[num-1])
                max_size = max(max_size, size)

        return max_size