Pen Box

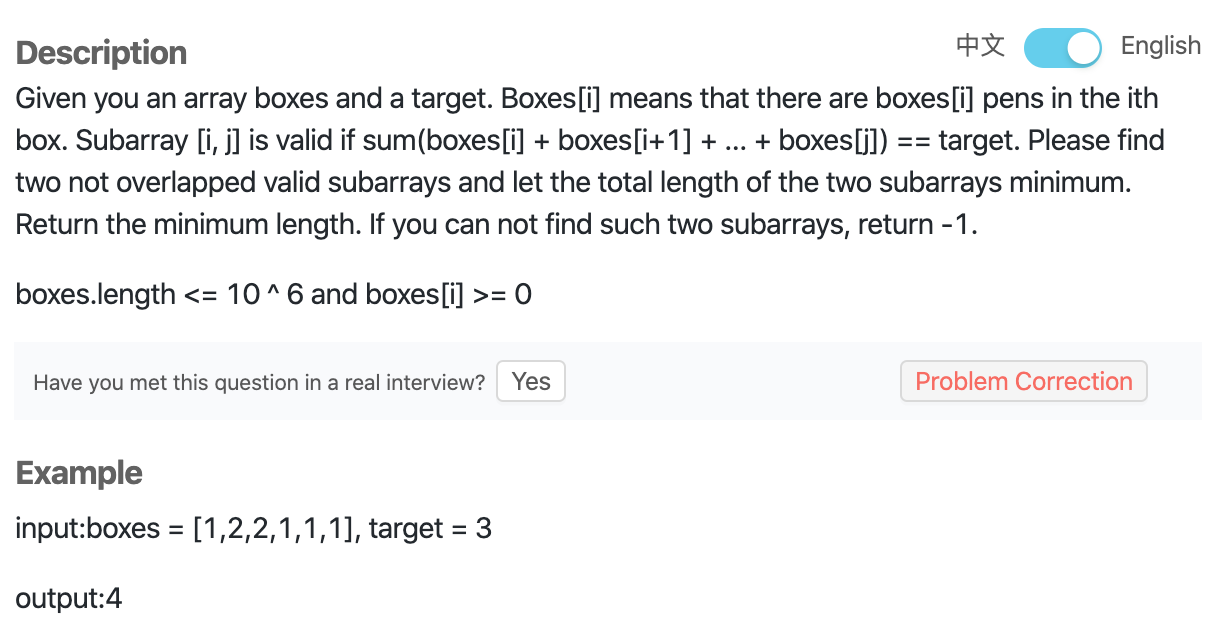
Solution

Brute-force solution would take $O(n^2)$: calculate sum of all subarrays, cut at a point and take the min.

DP & Two Pointers

Divide the boxes array into two parts, find_min_len in each part and return minimum left_min[i]+right_min[i+1].

Note:

• find_min_len only calculates the min lengths expanding from left for left_min, but can calculate right_min after boxes is reversed and result is reversed.
• csum means current sum.

def minimumBoxes(self, boxes, target):
    """
    @param boxes: number of pens for each box
    @param target: the target number
    @return: the minimum boxes
    """
    n = len(boxes)
    if n == 0:
        return -1

    left_min = self.find_min_len(boxes, target, n)
    boxes.reverse()
    right_min = self.find_min_len(boxes, target, n)
    right_min.reverse()

    res = sys.maxsize

    for i in range(n-1):
        res = min(res, left_min[i]+right_min[i+1])
    if res == sys.maxsize:
        return -1
    return res

def find_min_len(self, boxes, target, n):
    """
    returns an array in which each element records min length of subarray whose sum equals target
    """
    left_min = [sys.maxsize for _ in range(n)]
    # sum in current sliding window
    csum = 0
    left = 0

    # left == right == 0
    if csum == target:
        left_min[0] = 1
    for right in range(n):
        csum += boxes[right]
        # find window
        while csum > target:
            csum -= boxes[left]
            left += 1
        # eliminate leading 0's
        while left < right and boxes[left] == 0:
            left += 1
        # take last length if < target
        if csum < target:
            left_min[right] = left_min[right-1]
        # take shorter length if == target
        elif csum == target:
            left_min[right] = min(left_min[right-1], right-left+1)

    return left_min