Build Post Office II

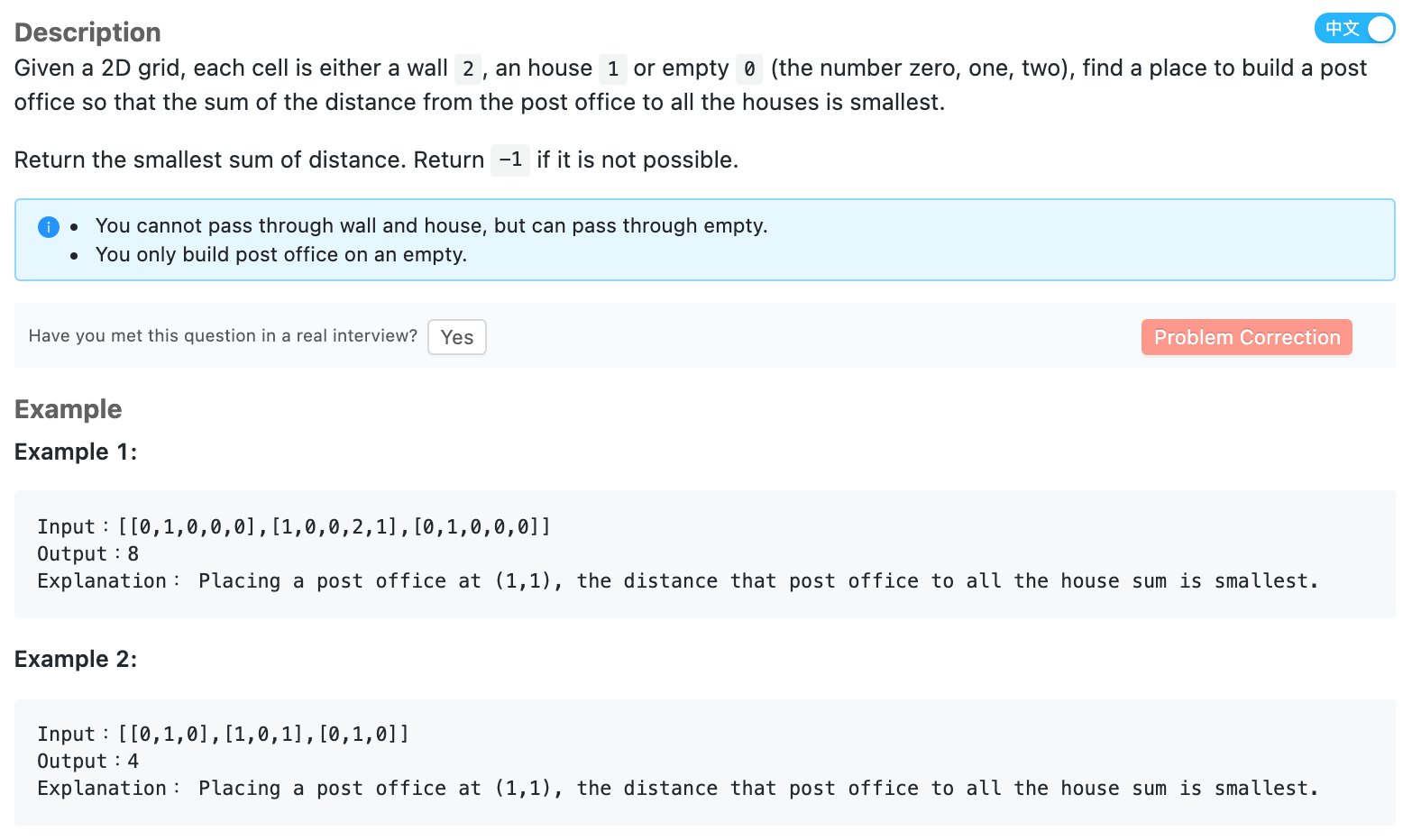
Input & Output

@param grid: a 2D grid
@return: An integer

Solution

Let $n$ be the number of rows and $m$ be the number of columns of grid.

Layered BFS

Rather than positioning the post office from empty spaces, we find it from houses.

For every empty space, we record:

1. how many houses can reach the position (counts incremented by $1$ if position is in range)
2. sum of steps to reach the position (dist)

If every space cannot be reached by all houses (counts[i][j]!=num_houses), then return $-1$; otherwise, there exists some space that can be reached by all houses, return the min summed distance.

Complexity

time: $O(V + E) = O(nm)$
space: $O(V + E) = O(nm)$

DIRECTIONS = [(1, 0), (-1, 0), (0, 1), (0, -1)]
def shortestDistance(self, grid):
    n, m = len(grid), len(grid[0])
    num_houses = 0
    res = sys.maxsize
    dist = [[sys.maxsize for _ in range(m)] for _ in range(n)]
    counts = [[0 for _ in range(m)] for _ in range(n)]

    def bfs(i, j):
        visited = [[False for _ in range(m)] for _ in range(n)]
        queue = [(i, j)]
        step = 0

        while queue:
            for _ in range(len(queue)):
                x, y = queue.pop(0)

                if dist[x][y] == sys.maxsize:
                    dist[x][y] = 0
                # dist incremented by # of layers
                dist[x][y] += step

                for dx, dy in DIRECTIONS:
                    nx, ny = x+dx, y+dy
                    # if position is in range, not visited, and a space
                    if 0 <= nx < n and 0 <= ny < m and visited[nx][ny] == False and grid[nx][ny] == 0:
                        visited[nx][ny] = True
                        # `counts` increments
                        counts[nx][ny] += 1
                        queue.append((nx, ny))

            # step increments
            step += 1

    # BFS from houses
    for i in range(n):
        for j in range(m):
            # point is a house
            if grid[i][j]==1:
                bfs(i, j)
                num_houses += 1

    for i in range(n):
        for j in range(m):
            # if every house can reach
            if counts[i][j] == num_houses and dist[i][j] < res:
                res = dist[i][j]

    return res if res!=sys.maxsize else -1