Sliding Puzzle

Input & Output

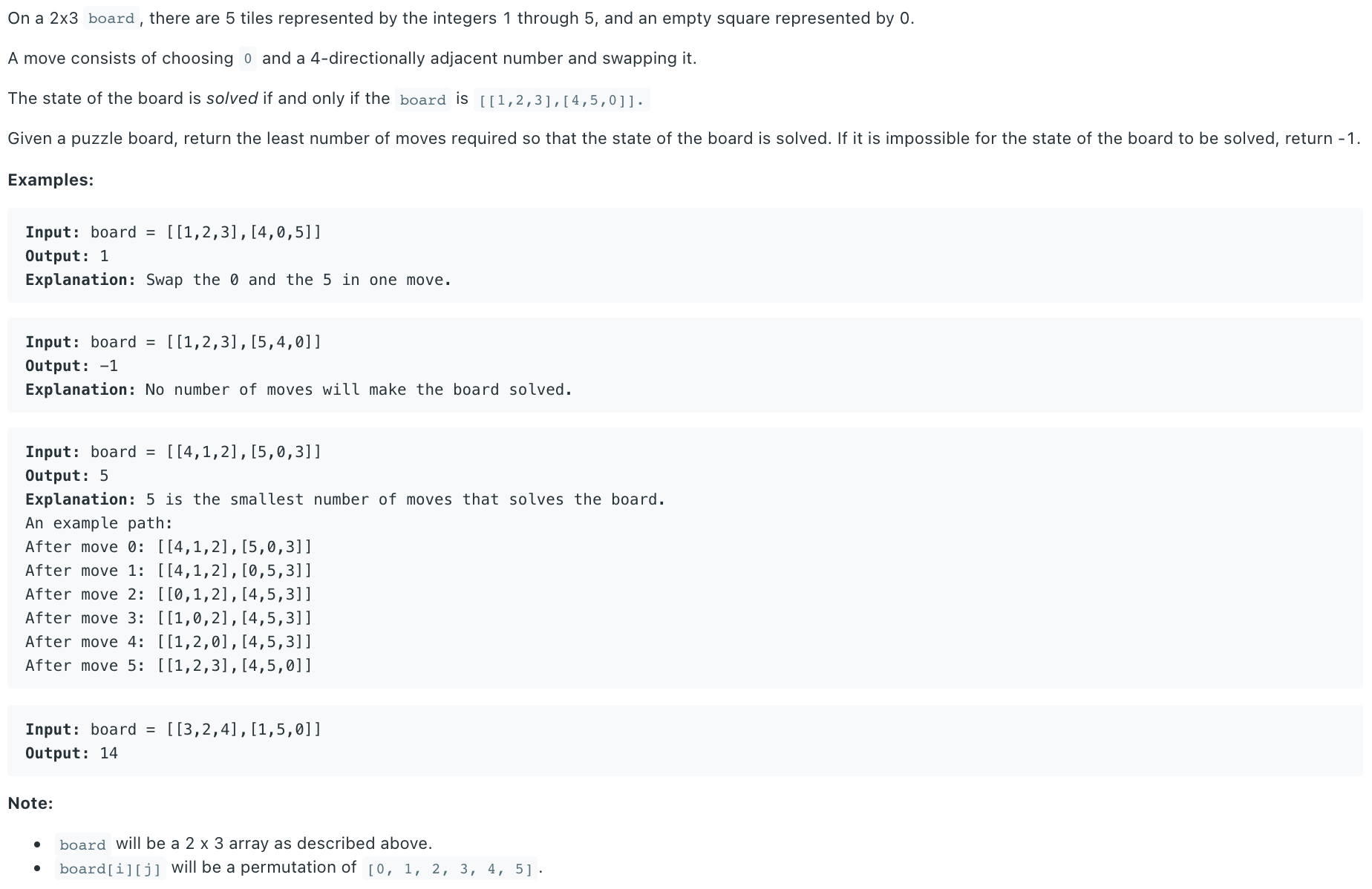
@param board: the given board
@return:  the least number of moves required so that the state of the board is solved

Solution

Let $n$ be the number of rows and $m$ be the number of columns of the board.

Complexity Analysis

Complexity

time: $O(nm \cdot (nm)!)$
space: $O(nm \cdot (nm)!)$

The number of possible states of the board is $(nm)!$. This is because there are $nm$ elements and you can choose one of the $nm$ elements for the first position, one of $nm-1$ for the next position $\cdots$. The search algorithm may visit every state once. It may do better, but big $O$ is an upper bound. The multiplier of nm is because to move from one state to the next makes a copy of the board, which takes $O(nm)$ time.

Layered BFS

DIRECTIONS = [(-1, 0), (1, 0), (0, -1), (0, 1)]
TARGET_STATE = "123450"
def slidingPuzzle(self, board: List[List[int]]) -> int:
    start = self.matrixToString(board)
    queue = [start]
    vis = set()
    res = 0

    while queue:
        for _ in range(len(queue)):
            state = queue.pop(0)
            if state == TARGET_STATE:
                return res
            for next_state in self.getNext(state):
                if next_state not in vis:
                    vis.add(next_state)
                    queue.append(next_state)
        res += 1
    return -1

def matrixToString(self, state_mat):
    state_str = ""
    for i in range(2):
        for j in range(3):
            state_str += str(state_mat[i][j])
    return state_str

def getNext(self, state):
    pos = state.find('0')
    x, y = pos // 3, pos % 3
    next_states = []
    for dx, dy in DIRECTIONS:
        nx, ny = x + dx, y + dy
        if 0<=nx<2 and 0<=ny<3:
            npos = 3*nx + ny
            mn, mx = min(pos, npos), max(pos, npos)
            nstate = state[:mn] + state[mx] + state[mn+1:mx] + state[mn] + state[mx+1:]
            next_states.append(nstate)
    return next_states

Or more succinctly, using tuple rather than str to encode board:

def slidingPuzzle(self, board: List[List[int]]) -> int:
    n, m = len(board), len(board[0])
    start = tuple(itertools.chain(*board))
    queue = [(start, start.index(0))]
    vis = set()
    end = tuple([i for i in range(1, n*m)] + [0])
    res = 0

    while queue:
        for _ in range(len(queue)):
            board, pos = queue.pop(0)
            if board == end:
                return res
            for d in (-1, 1, -m, m):
                npos = pos + d
                # ensure only move by 1 in any direction
                if abs(npos//m - pos//m) + abs(npos%m - pos%m) != 1:
                    continue
                if 0 <= npos < n*m:
                    nboard = list(board)
                    nboard[pos], nboard[npos] = nboard[npos], nboard[pos]
                    nboard = tuple(nboard)
                    if nboard not in vis:
                        vis.add(nboard)
                        queue.append((nboard, npos))
        res += 1

    return -1

A* Algorithm

$f = g + h$, where $f$ is the estimated distance (priority), $g$ is the actual distance travelled from start node (depth), and $h$ is the heuristic distance to the end node.

from heapq import heappush, heappop
from collections import defaultdict
def slidingPuzzle(self, board: List[List[int]]) -> int:
    n, m = len(board), len(board[0])
    start = tuple(itertools.chain(*board))
    pqueue = [(0, 0, start, start.index(0))]
    vis = set()
    end = tuple([i for i in range(1, n*m)] + [0])
    end_wrong = tuple([i for i in range(1, n*m-2)] + [n*m-1, n*m-2, 0])
    cost = defaultdict(lambda: sys.maxsize)
    cost[start] = 0
    expected = {(m*i+j+1) % (n*m): (i, j) for i in range(n) for j in range(m)}

    def heuristic(board):
        h = 0
        for i in range(n):
            for j in range(m):
                val = board[m*i + j]
                if val == 0: continue
                ei, ej = expected[val]
                h += abs(i - ei) + abs(j - ej)
        return h

    while pqueue:
        f, g, board, pos = heappop(pqueue)
        if board == end: return g
        if board == end_wrong: return -1
        if f > cost[board]: continue

        for d in (-1, 1, -m, m):
            npos = pos + d
            if abs(npos//m - pos//m) + abs(npos%m - pos%m) != 1:
                continue
            if 0 <= npos < n*m:
                nboard = list(board)
                nboard[pos], nboard[npos] = nboard[npos], nboard[pos]
                nboard = tuple(nboard)
                nf = g + 1 + heuristic(nboard)
                if nf < cost[nboard]:
                    cost[nboard] = nf
                    heappush(pqueue, (nf, g+1, nboard, npos))
    return -1