Median of Two Sorted Arrays

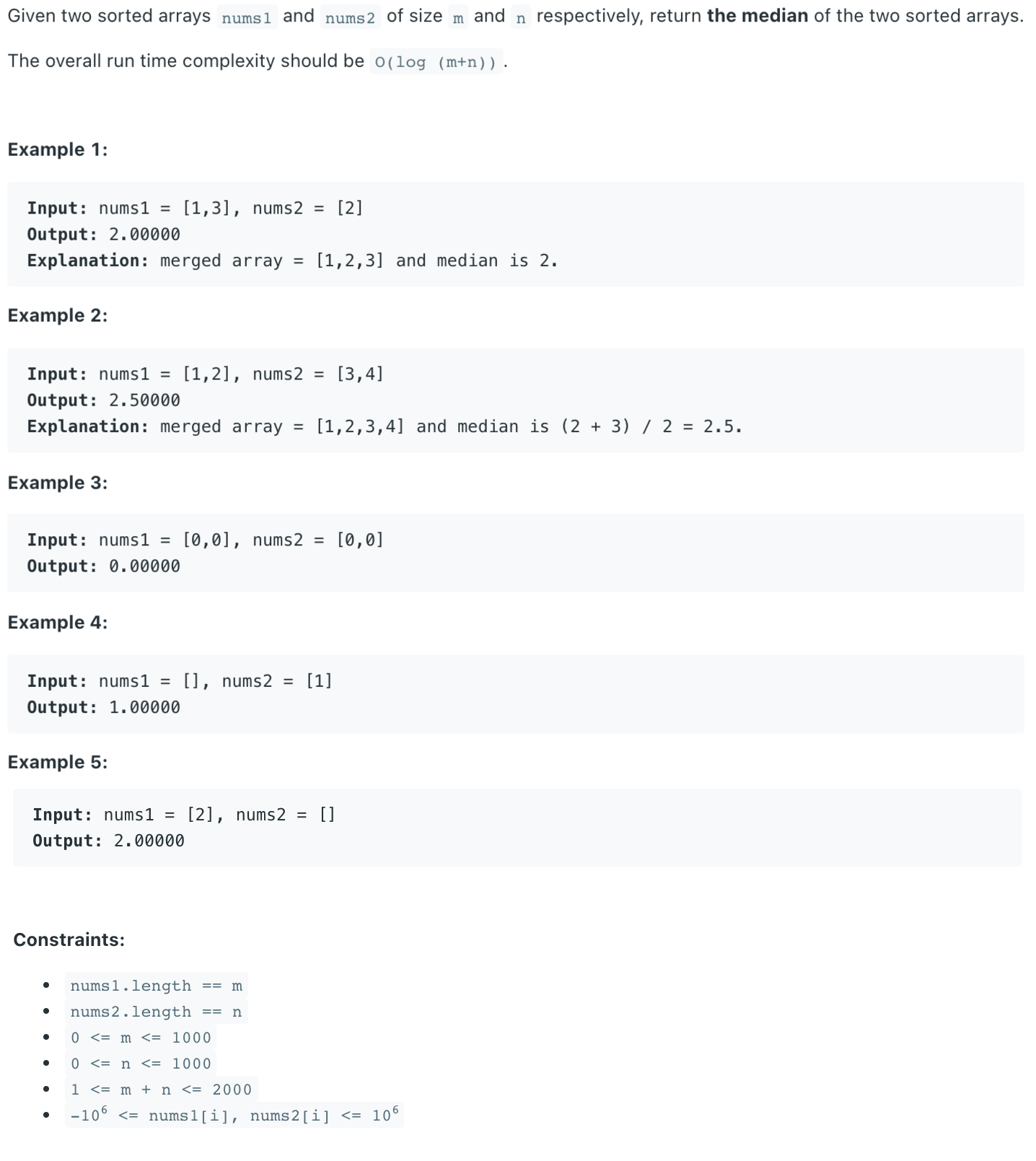
Solution

Let $m$ be the length of nums1 and $n$ be the length of nums2.

Brute Force

Merge nums1 and nums2 into sorted nums, and find the median.

Complexity

time: $O(m + n)$
space: $O(m + n)$

def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:
    nums = []
    m, n = len(nums1), len(nums2)
    i = j = 0
    while i < m or j < n:
        if j == n or i < m and nums1[i] < nums2[j]:
            nums.append(nums1[i])
            i += 1
        else:
            nums.append(nums2[j])
            j += 1
    l = len(nums)
    return nums[l//2] if l % 2 else (nums[l//2 - 1] + nums[l//2])/2

Follow Up

The overall run time complexity should be $O(\log (m+n))$.

Binary Search (REDO)

This video (opens new window) and This post in Chinese (opens new window) explains well.

Complexity

time: $O(\log(\min(m, n)))$
space: $O(1)$

def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:
    m, n = len(nums1), len(nums2)
    # nums1 should be shorter than nums2, s.t. `partitionY` is always nonnegative
    if n < m:
        nums1, nums2 = nums2, nums1
        m, n = n, m
    low, high = 0, len(nums1)
    while low <= high:
        partitionX = (low + high) // 2
        partitionY = (m + n + 1) // 2 - partitionX
        leftMaxX = -sys.maxsize if partitionX == 0 else nums1[partitionX - 1]
        rightMinX = sys.maxsize if partitionX == m else nums1[partitionX]
        leftMaxY = -sys.maxsize if partitionY == 0 else nums2[partitionY - 1]
        rightMinY = sys.maxsize if partitionY == n else nums2[partitionY]
        # partitionX found, return the median
        if leftMaxX <= rightMinY and leftMaxY <= rightMinX:
            # if the total length is odd, then return the left max
            if (m + n) % 2:
                return max(leftMaxX, leftMaxY)
            # if the total length is even, then return the average of the left max and right min
            else:
                return (max(leftMaxX, leftMaxY) + min(rightMinX, rightMinY)) / 2
        # partitionX is too much to the right
        elif leftMaxX > rightMinY:
            high = partitionX - 1
        # partitionX is too much to the left
        else:
            low = partitionX + 1
    raise Exception("Arguments were not sorted!")