Multiply Strings

Solution

Let $n$ be the length of string num1 and $m$ be the length of string num2.

Both solutions below use the following grade-school algorithm for multiplication:

EPI in Python, page 44

Multiply the 1st number by each digit of the second, and then add all the resulting terms.

From a space perspective, it is better to incrementally add the terms rather than compute all of them individually and then add them up. The number of digits required for the product is at most $n + m$ for $n$ and $m$ digit operands, so we use an array of size $n + m$ for the result.

int Array $\rightarrow$ String

Use an int array to store the result and convert back to string.

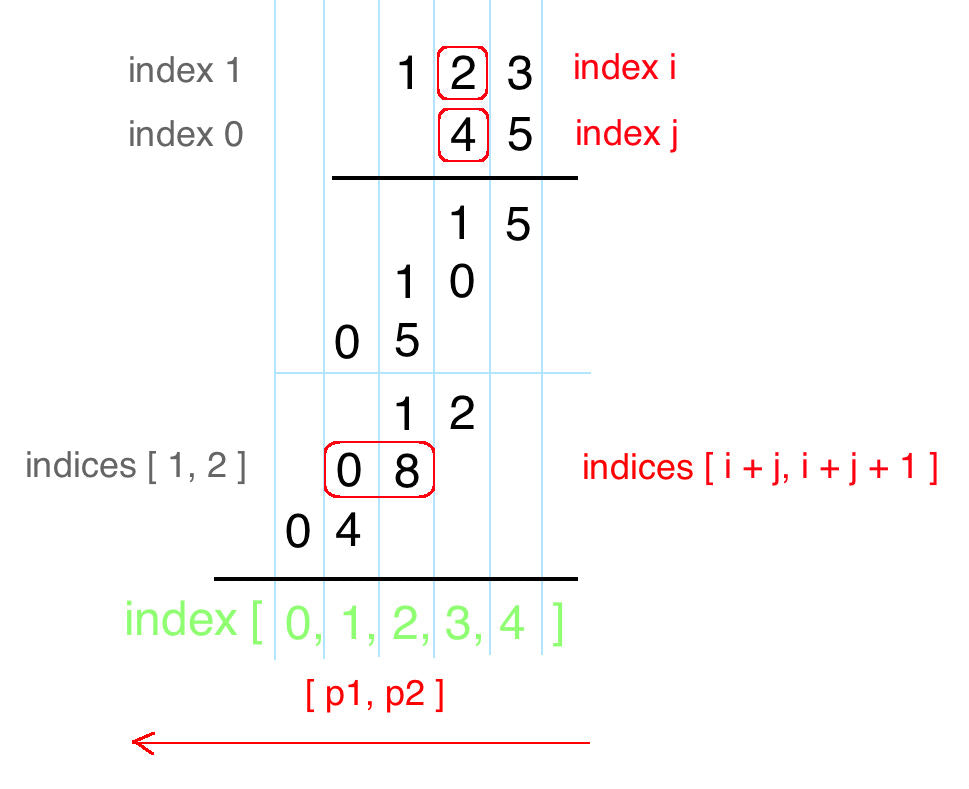
num1[i] * num2[j] will be placed at prod[i+j] and prod[i+j+1].

Complexity

time: $O(n + m)$
space: $O(n + m)$

def multiply(self, num1: str, num2: str) -> str:
    if num1 == "0" or num2 == "0":
        return "0"

    n, m = len(num1), len(num2)
    prod = [0 for _ in range(n+m)]

    for i in reversed(range(n)):
        for j in reversed(range(m)):
            pos1, pos2 = i+j, i+j+1
            prod[i+j+1] += int(num1[i]) * int(num2[j])
            prod[i+j] += prod[i+j+1] // 10
            prod[i+j+1] %= 10

    res = ""
    for i, p in enumerate(prod):
        if not (i == 0 and p == 0):
            res += str(p)
    return res

Modify String as char Array

Calculate product of int digits and store in string csum.

Since strings in Python cannot be modified, following solution is in C++:

Complexity

time: $O(n + m)$
space: $O(1)$

string multiply(string num1, string num2) {
    string csum(num1.size() + num2.size(), '0');

    for (int i = num1.size() - 1; 0 <= i; --i) {
        int carry = 0;
        for (int j = num2.size() - 1; 0 <= j; --j) {
            int tmp = (csum[i+j+1] - '0') + (num1[i] - '0') * (num2[j] - '0') + carry;
            csum[i+j+1] = tmp%10 + '0';
            carry = tmp / 10;
        }
        csum[i] += carry;
    }

    size_t startpos = csum.find_first_not_of("0");
    if (string::npos != startpos) {
        return csum.substr(startpos);
    }
    return "0";
}