Sqrt(x)

Solution

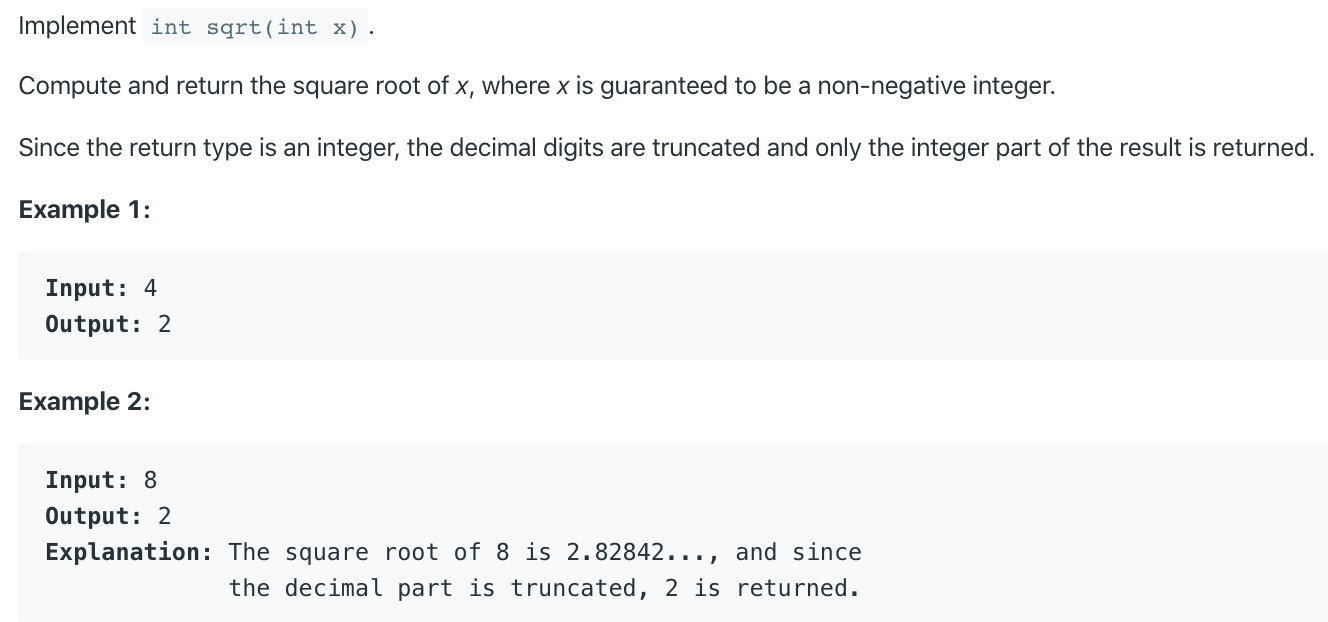
There are so many of them! Thanks to this question that I review Newton's method in Calculus.

Binary search may be easiest to write in an interview.

Pocket Calculator Algorithm

Based on the formula (hard to come up with if haven't seen before):

$\sqrt{x} = e^{\frac{1}{2}\log x}$

Complexity

time: $O(1)$
space: $O(1)$

from math import e, log
def mySqrt(self, x):
    if x < 2:
        return x

    left = int(e**(0.5 * log(x)))
    right = left + 1
    return left if right * right > x else right

Binary Search

If $x < 2$, return $x$.

For $x \ge 2$, $\sqrt{x}$ is always smaller than $\frac{x}{2}$ and larger than 0: $0 < a < \frac{x}{2}$.

Complexity

time: $O(\log N)$
space: $O(1)$

def mySqrt(self, x):
    if x < 2:
        return x

    left, right = 2, x // 2

    while left <= right:
        pivot = left + (right - left) // 2
        num = pivot * pivot
        if num > x:
            right = pivot -1
        elif num < x:
            left = pivot + 1
        else:
            return pivot

    return right

Recursion + Bit Shifts

Because $\sqrt{x} = 2 \times \sqrt{\frac{x}{4}}$, we can do a recursion:

$mySqrt(x) = 2 \times mySqrt(\frac{x}{4})$

Could continue to optimize by bit shifts:

$mySqrt(x)=mySqrt(x> >2)< <1$

def mySqrt(self, x):
    if x < 2:
        return x

    left = self.mySqrt(x >> 2) << 1
    right = left + 1
    return left if right * right > x else right

Newton's Method

Newton's method (opens new window) gives the best runtime asymptotically:

The math is deduced below:

$x_{n+1}=x_{n}-\frac{f\left(x_{n}\right)}{f^{\prime}\left(x_{n}\right)}=x_{n}-\frac{x_{n}^{2}-a}{2 x_{n}}=\frac{1}{2}\left(x_{n}+\frac{a}{x_{n}}\right)$

The following 3 solutions all use Newton's method in different forms.

initialize sqrt to x//2

Given the fact in binary search, return x if x < 2; otherwise, x//2 is an upper bound for $\texttt{int} \sqrt{x}$ and the in the while loop sqrt monotonically decreases in every iteration.

    def mySqrt(self, x: int) -> int:
        if (x<2): return x
        sqrt = x//2
        while not (sqrt*sqrt<=x and (sqrt+1)**2>x):
            sqrt = (sqrt + x//sqrt)//2
        return sqrt

initialize sqrt to x

In the while loop, sqrt monotonically decreases in every iteration.

    def mySqrt(self, x: int) -> int:
        sqrt = x
        while sqrt**2>x:
            sqrt = (sqrt + x//sqrt)//2
        return sqrt

initialize y & z

The proof is sinuous and runtime is slower than the previous two solutions.

    def mySqrt(self, x: int) -> int:
        y = 1
        z = x
        while z > y:
            z = (z+y)//2
            y = x//z
        return z

Fast Approximations for Floating Sqrt

According to this video (opens new window), the floating sqrt can be approximated by the following methods.

Continued Fraction

First approximate $x$ as $a^2 + b$, where $a^2 \gg b$. Then:

$x = a + \frac{b}{2a + \frac{b}{2a + \frac{b}{2a + \cdots}}}$

Proof

$\begin{aligned} s &= a^2 + b \\ s - a^2 &= b \\ (\sqrt{s} + a)(\sqrt{s} - a) &= b \\ \sqrt{s} - a &= \frac{b}{\sqrt{s} + a} \\ \sqrt{s} &= a + \frac{b}{a + \sqrt{s}} \\ \text{recursively plug in } s \rightarrow \sqrt{s} &= a + \frac{b}{a + a + \frac{b}{a + \sqrt{s}}} = a + \frac{b}{2a + \frac{b}{a + \sqrt{s}}} \end{aligned}$

Long Division

Starting from 4:50 (opens new window), the method is presented.