Knight Shortest Path II

Input & Output

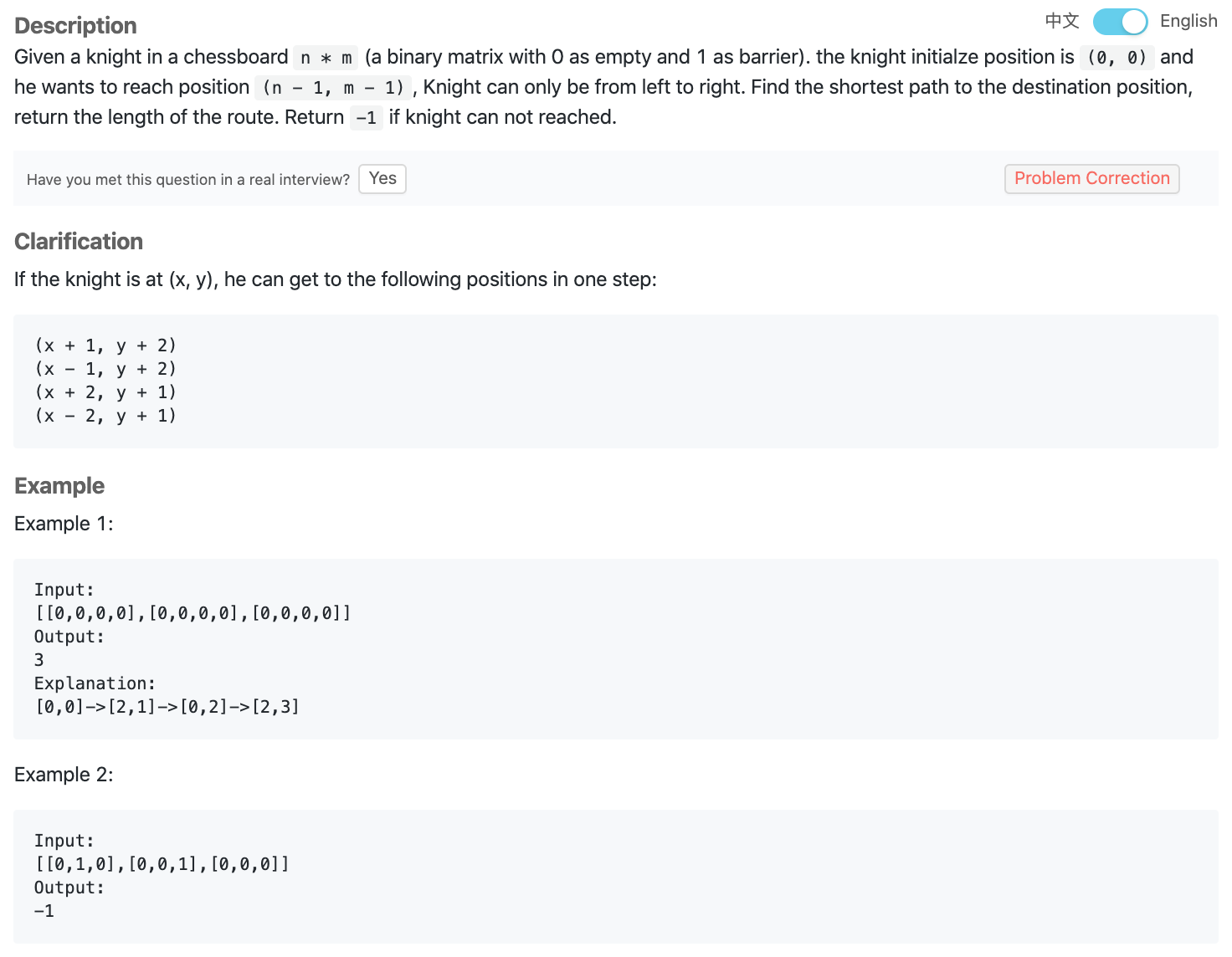
@param {boolean[][]} grid a chessboard included 0 and 1
@return {int} the shortest path

Solution

Let $n$ be the number of rows and $m$ be the number of columns. All following solutions take $O(V + E) = O(nm)$ time and space.

BFS w/ HashMap

Use queue to visit nodes and dist(could also be an array or hashset instead of hashmap) to store the distance of reaching a point.

DIRECTIONS = [(1,2), (-1, 2), (2,1), (-2, 1)]
def shortestPath2(self, grid):
    n = len(grid)
    m = len(grid[0])
    if n == 0 or m == 0:
        return -1

    queue = []
    queue.append((0, 0))
    dist = {}
    dist[(0, 0)] = 0
    last_pt = {}
    last_pt[(0, 0)] = (-1, -1)

    while queue:
        x, y = queue.pop(0)
        for dx, dy in DIRECTIONS:
            nx, ny = x+dx, y+dy
            if self.is_valid(nx, ny, grid, dist):
                queue.append((nx, ny))
                dist[(nx, ny)] = dist[(x, y)] + 1
                last_pt[(nx, ny)] = (x, y)
    if (n-1, m-1) in dist:
        path = self.find_path(n, m, grid, last_pt)
        return dist[(n-1, m-1)]
    return -1

def is_valid(self, x, y, grid, dist):
    if not 0<= x <len(grid) or not 0<= y <len(grid[0]):
        return False
    if grid[x][y] == 1:
        return False
    if (x, y) in dist:
        return False
    return True

def find_path(self, n, m, grid, last_pt):
    pt = (n-1, m-1)
    path = []
    while pt in last_pt:
        path.append(pt)
        pt = last_pt[pt]
    path.reverse()
    return path

Follow Up

output any shortest path

To output a path, we need to store the last point for each current point. We can't do the reverse b/c there might be multiple next points for each current point.

The added code is highlighted in BFS w/ HashMap code above.

output a shortest path in alphabetical order

To follow alphabetical order, we need to use heapq to replace the original queue w/ a priority queue. Added or changed lines are highlighted.

In is_valid, if the old way of visiting, dist[(x, y)], has smaller distance than that of the new way of visiting, last_dist + 1, then new way doesn't shorten the path, and we don't want to visit (nx, ny) again.

DIRECTIONS = [(1,2), (-1, 2), (2,1), (-2, 1)]
import heapq
def shortestPath2(self, grid):
    n = len(grid)
    m = len(grid[0])
    if n == 0 or m == 0:
        return -1

    queue = []
    heapq.heappush(queue, (0, 0))
    dist = {}
    dist[(0, 0)] = 0
    last_pt = {}
    last_pt[(0, 0)] = (-1, -1)

    while queue:
        x, y = heapq.heappop(queue)
        for dx, dy in DIRECTIONS:
            nx, ny = x+dx, y+dy
            last_dist = dist[(x,y)]
            if self.is_valid(nx, ny, grid, dist, last_dist):
                heapq.heappush(queue, (nx, ny))
                dist[(nx, ny)] = dist[(x, y)] + 1
                last_pt[(nx, ny)] = (x, y)
    if (n-1, m-1) in dist:
        path = self.find_path(n, m, grid, last_pt)
        return dist[(n-1, m-1)]
    return -1

def is_valid(self, x, y, grid, dist, last_dist):
    if not 0 <= x < len(grid) or not 0 <= y < len(grid[0]):
        return False
    if grid[x][y] == 1:
        return False
    # if the old ways exists and is shorter than the new way
    if (x, y) in dist and dist[(x, y)] <= last_dist+1:
        return False
    return True

def find_path(self, n, m, grid, last_pt):
    pt = (n-1, m-1)
    path = []
    while pt in last_pt:
        path.append(pt)
        pt = last_pt[pt]
    path.reverse()
    return path

Bidirectional BFS (Optional)

Instead of doing BFS in 1 direction, we can start from source and destination. A path is found when these 2 searches meet.

The time and space complexities do not improve.

from collections import deque
def shortestPath2(self, grid):
    if grid == [[]] or len(grid) == 0:
        return -1

    m = len(grid)
    n = len(grid[0])

    if grid[0][0] or grid[m - 1][n - 1]:
        return -1

    if m == 1 and n == 1:
        return 0

    queue_A = deque()
    visited_A = [[False for _ in range(n)] for _ in range(m)]
    queue_A.append([0,0])
    visited_A[0][0] = True

    queue_B = deque()
    visited_B = [[False for _ in range(n)] for _ in range(m)]
    queue_B.append([m - 1, n - 1])
    visited_B[m - 1][n - 1] = True

    queue = deque()
    visited_Curr = [[False for _ in range(n)] for _ in range(m)]
    visited_Other_pos = [[False for _ in range(n)] for _ in range(m)]

    res = 0
    sign = 0 # 1 if from left to right / -1 if from right to left

    dx = [-1, 1, -2, 2]
    dy = [2, 2, 1, 1]

    # bfs
    while queue_A and queue_B:

        if len(queue_A) <= len(queue_B):
            queue = queue_A
            visited_Curr = visited_A
            visited_Other_pos = visited_B
            sign = 1
        else:
            queue = queue_B
            visited_Curr = visited_B
            visited_Other_pos = visited_A
            sign = -1

        res += 1

        for _ in range(len(queue)):
            x, y = queue.popleft()
            for i in range(4):
                newx = x + sign * dx[i]
                newy = y + sign * dy[i]
                if self.isValid(newx, m, newy, n, grid):
                    if visited_Other_pos[newx][newy] :
                        return res

                    if not visited_Curr[newx][newy]:
                        queue.append([newx, newy])
                        visited_Curr[newx][newy] = True

    return -1

def isValid(self, x, m, y, n, grid):
    if 0 <= x < m and 0 <= y < n:
        return False

    if grid[x][y] == 1:
        return False

    return True

DP

The array dist stores the shortest distance to get to a point, so initialize dist[0][0] to be $0$ and the rest to be sys.maxsize.

Note that we should iterate column before row, b/c knight could only go from left to right. Otherwise, some dist element may be calculated while its dependent elements are still sys.maxsize.

DIRECTIONS = [(-1, -2), (1, -2), (-2, -1), (2, -1)]
def shortestPath2(self, grid):
    n = len(grid)
    m = len(grid[0])

    if not n or not m: return -1
    dist = [[sys.maxsize for _ in range(m)] for _ in range(n)]
    dist[0][0] = 0

    for j in range(m):
        for i in range(n):
            if grid[i][j]==1:
                continue
            for dx, dy in DIRECTIONS:
                nx, ny = i + dx, j + dy
                if 0 <= nx < n and 0 <= ny < m:
                    dist[i][j] = min(dist[i][j], dist[nx][ny] + 1)

    return -1 if dist[n-1][m-1] == sys.maxsize else dist[n-1][m-1]