Binary Tree Maximum Path Sum

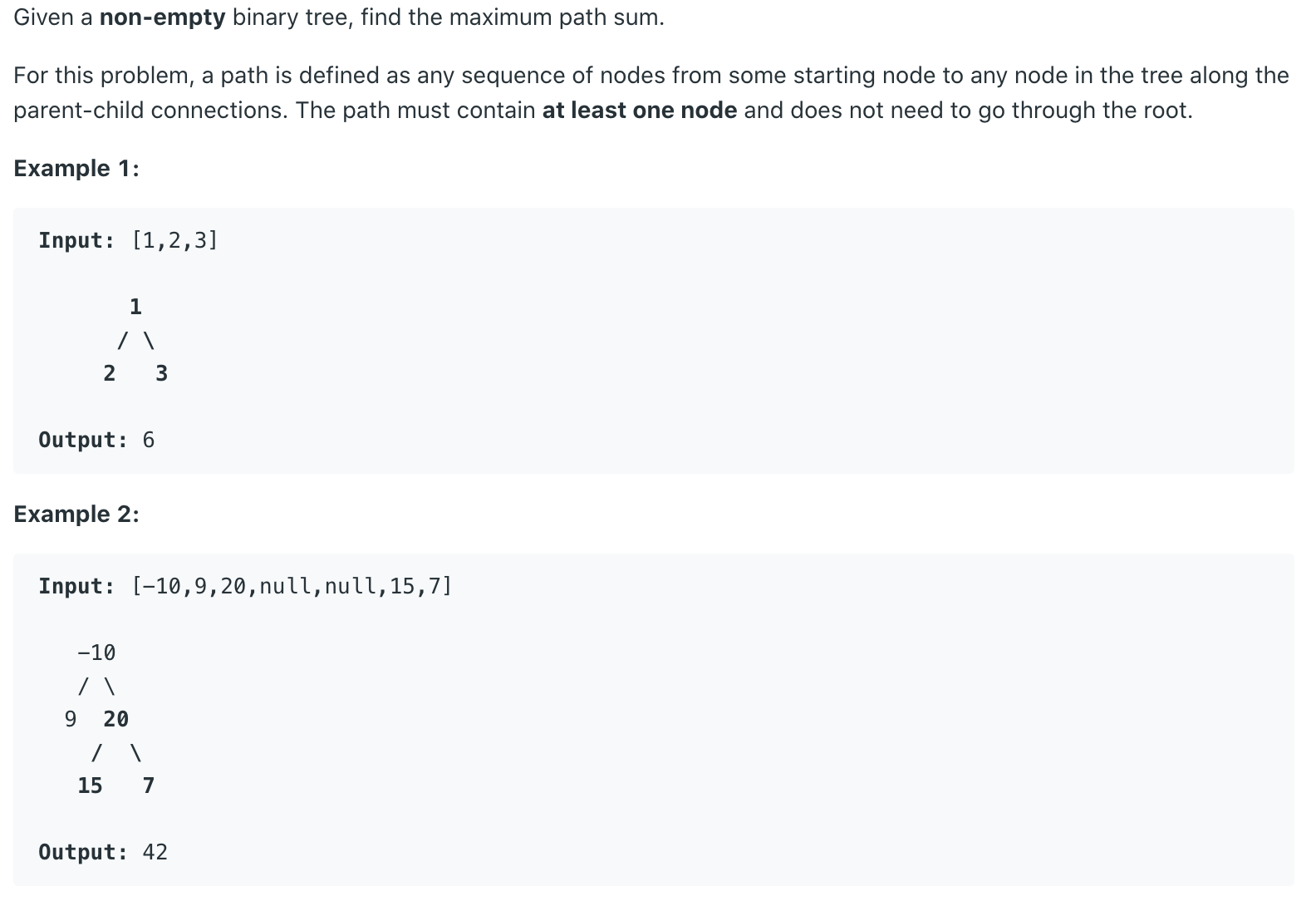
Definition for a Binary Tree Node

class TreeNode:
    def __init__(self, val):
        self.val = val
        self.left, self.right = None, None

Solution

Recursive DFS

Return 2 values in dfs:

1. max_sum is the sum of a whole tree (left, right, or current)
2. max_chain is sum of current node plus either the left or the right sub-tree

At the end, return the max_sum of root, as root must be included.

def maxPathSum(self, root: TreeNode) -> int:
    def dfs(root):
        if not root: return (-sys.maxsize, 0)

        left_max_sum, left_max_chain = dfs(root.left)
        right_max_sum, right_max_chain = dfs(root.right)
        max_sum = max(left_max_sum, right_max_sum, left_max_chain + right_max_chain + root.val)
        max_chain = max(max(left_max_chain, right_max_chain) + root.val, 0)
        return (max_sum, max_chain)

    return dfs(root)[0]

Improved Recursive DFS

This solution has similar logic but easier to understand. Update res if max_sum is larger. Return max_chain.

def maxPathSum(self, root: TreeNode) -> int:
    def dfs(node):
        nonlocal res
        if not node:
            return 0
        # max sum on left/right sub-trees of node
        left_sum = max(dfs(node.left), 0)
        right_sum = max(dfs(node.right), 0)

        max_sum = node.val + left_sum + right_sum
        res = max(res, max_sum)
        return node.val + max(left_sum, right_sum)

    res = -sys.maxsize
    dfs(root)
    return res