Kth Largest Element in an Array

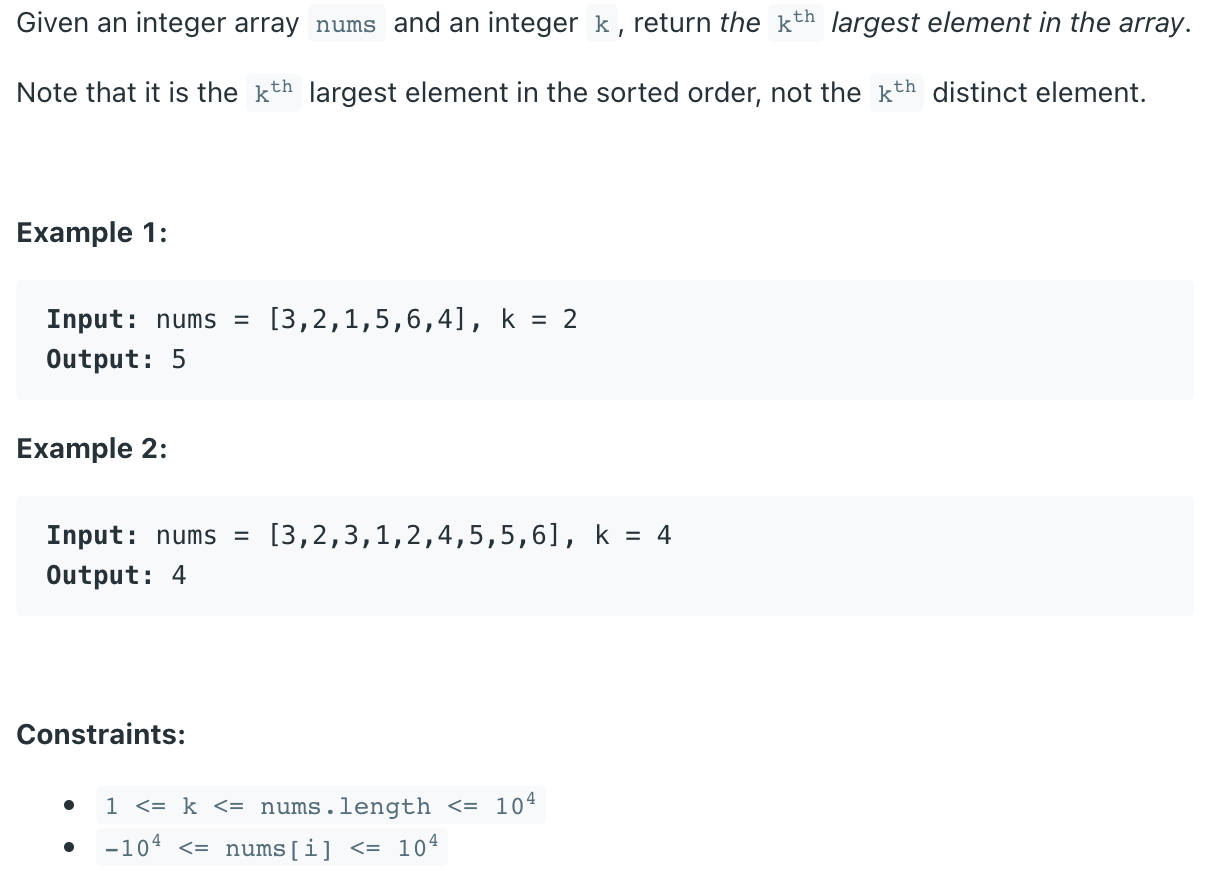
Solution

Let $n$ be the length of the array.

1-liner Cheating

Use sorted:

def findKthLargest(self, nums: List[int], k: int) -> int:
    n = len(nums)
    return sorted(nums)[n-k]

Or use built-in heapq:

def findKthLargest(self, nums: List[int], k: int) -> int:
    return heapq.nlargest(k, nums)[-1]

Heap

Complexity

time: $O(n)$
space: $O(k)$

from heapq import heappush
def findKthLargest(self, nums: List[int], k: int) -> int:
    n = len(nums)
    heap = []
    for i in range(n):
        heappush(heap, nums[i])
        if len(heap) > k:
            heappop(heap)
    return heappop(heap)

Quick Select

Complexity

time: $O(n)$ (worst case: $O(n^2)$)
space: $O(n)$

Lomuto Partition

def findKthLargest(self, nums: List[int], k: int) -> int:

    def partition(arr, left, right):
        # move pivot to the end
        pivot = arr[right]
        store_idx = left
        for i in range(left, right):
            # move elt smaller than pivot to the left
            if arr[i] < pivot:
                arr[store_idx], arr[i] = arr[i], arr[store_idx]
                store_idx += 1

        arr[store_idx], arr[right] = arr[right], arr[store_idx]
        return store_idx

    def quickSelect(arr, left, right, k):
        if left == right:
            return arr[left]
        pivot_idx = partition(arr, left, right)
        if k == pivot_idx:
            return arr[k]
        if k < pivot_idx:
            return quickSelect(arr, left, pivot_idx-1, k)
        else:
            return quickSelect(arr, pivot_idx+1, right, k)

    n = len(nums)
    return quickSelect(nums, 0, n-1, n-k)

Hoare Partition

def findKthLargest(self, nums: List[int], k: int) -> int:

    def partition(arr, left, right):
        pivot = arr[right]
        i, j = left, right
        while True:
            while arr[i] < pivot:
                i += 1
            while j > 0 and arr[j] >= pivot:
                j -= 1

            # if two pointers meet
            if i >= j:
                break
            else:
                arr[i], arr[j] = arr[j], arr[i]
        arr[i], arr[right] = arr[right], arr[i]
        return i

    def quickSelect(arr, left, right, k):
        if left == right:
            return arr[left]
        pivot_idx = partition(arr, left, right)
        if k == pivot_idx:
            return arr[k]
        if k < pivot_idx:
            return quickSelect(arr, left, pivot_idx-1, k)
        else:
            return quickSelect(arr, pivot_idx+1, right, k)

    n = len(nums)
    return quickSelect(nums, 0, n-1, n-k)