Knight Shortest Path

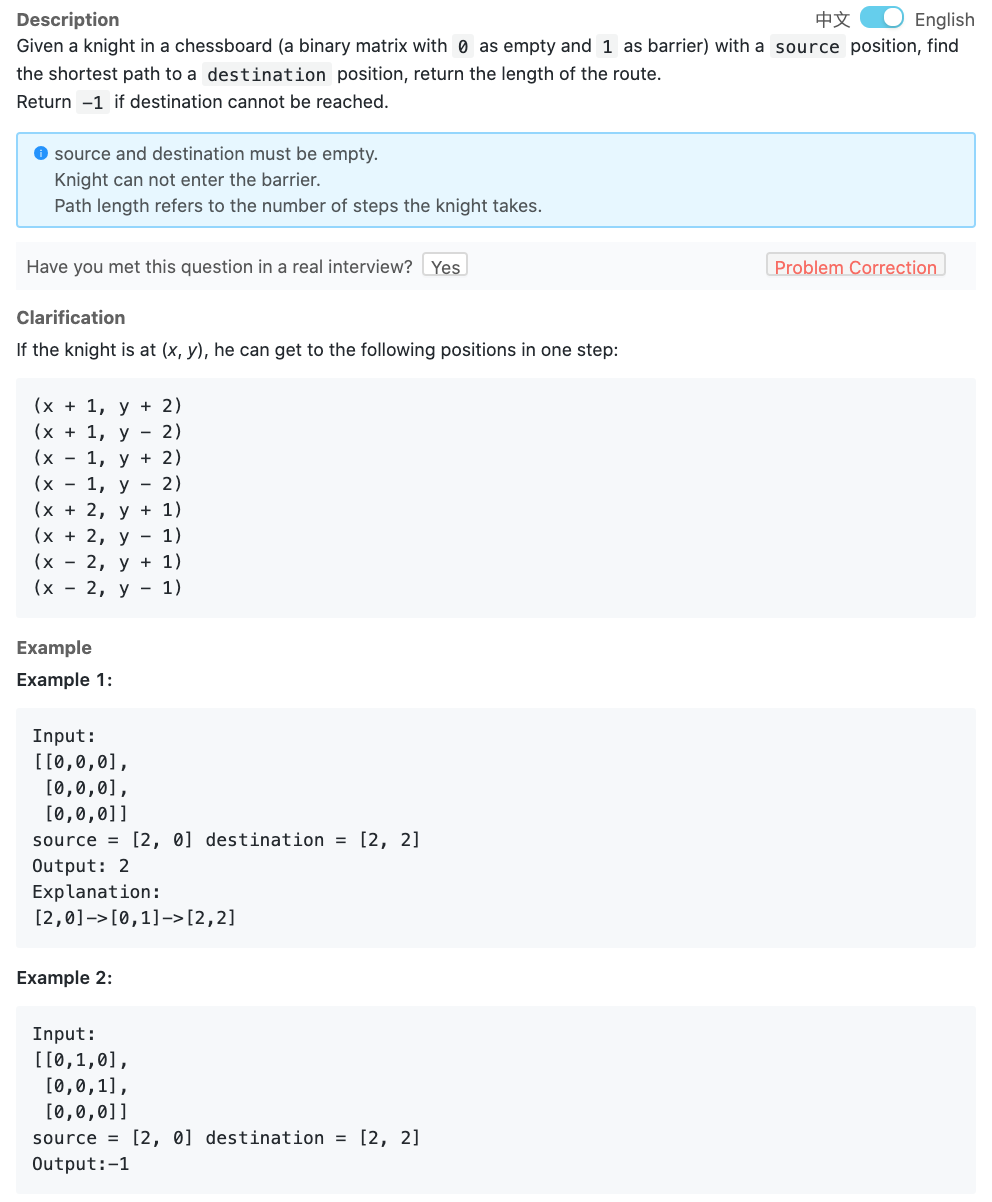
Input & Output

@param grid: a chessboard included 0 (false) and 1 (true)
@param source: a point
@param destination: a point
@return: the shortest path

Solution

Let $n$ be the number of rows and $m$ be the number of columns. All following solutions take $O(V + E) = O(nm)$ time and space.

Definition for a point

class Point:
    def __init__(self, a=0, b=0):
        self.x = a
        self.y = b

BFS w/ HashMap

Use queue to visit nodes and dist(could also be an array or hashset instead of hashmap) to store the distance of reaching a point.

DIRECTIONS = [(-1, -2), (-1, 2), (1, -2), (1, 2), (-2, -1), (-2, 1), (2, -1), (2, 1)]
def shortestPath(self, grid, source, destination):
    n, m = len(grid), len(grid[0])
    if not n or not m: return -1
    queue = [(source.x, source.y)]
    dist = {(source.x, source.y): 0}

    while queue:
        x, y = queue.pop(0)
        if (x, y)==(destination.x, destination.y):
            return dist[(x, y)]
        for dx, dy in DIRECTIONS:
            nx, ny = x + dx, y + dy
            if self.is_valid(n, m, nx, ny, grid, dist):
                queue.append((nx, ny))
                dist[(nx, ny)] = dist[(x, y)] + 1
    return -1

def is_valid(self, n, m, x, y, grid, dist):
    if not 0 <= x < n or not 0 <= y < m:
        return False
    return grid[x][y]!=1 and (x, y) not in dist