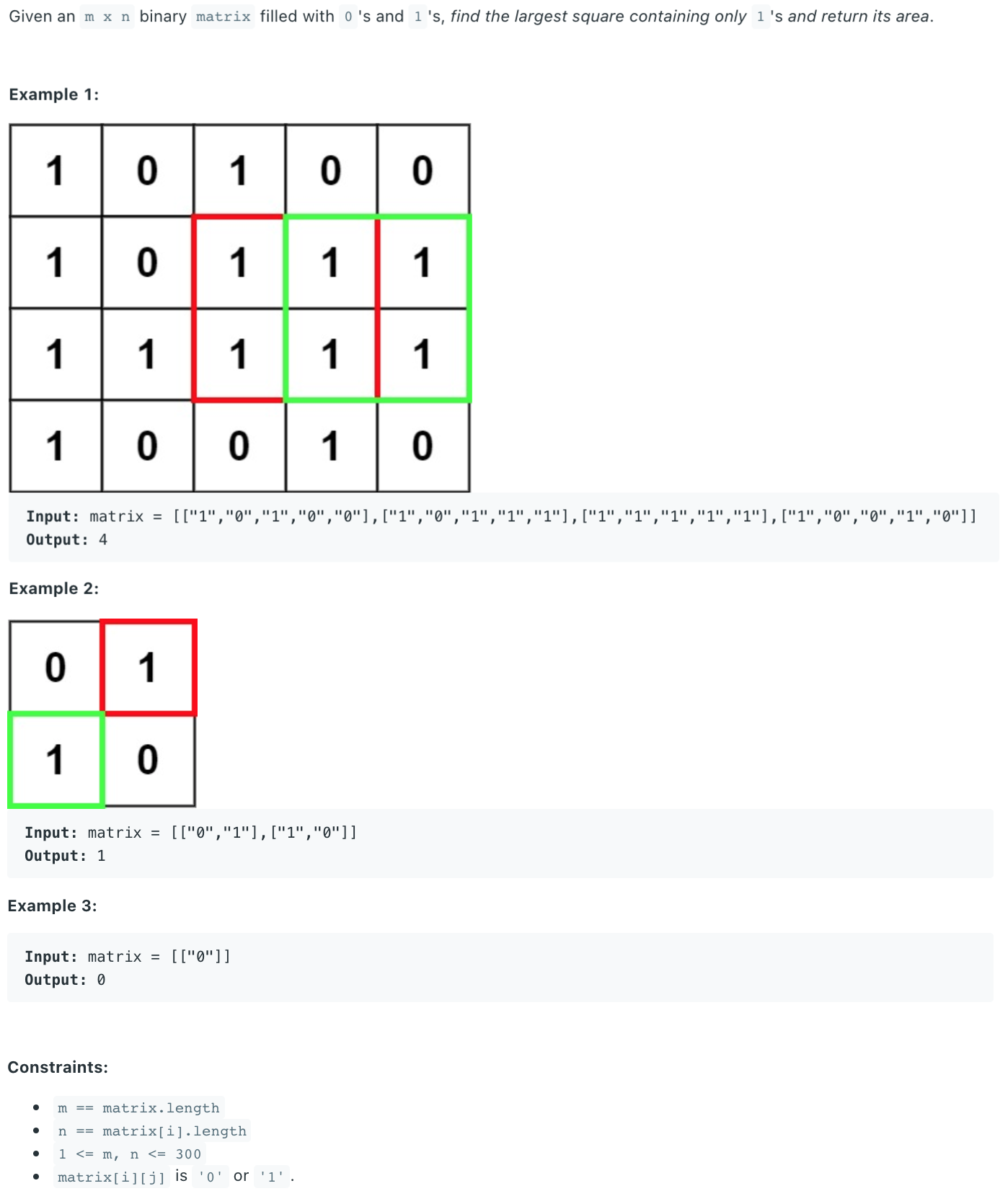
Maximal Square

Solution

Let $n$ be the number of rows and $m$ be the number of columns.

The state transition holds only when matrix[i][j] == '1':
dp[i, j] = min(dp[i-1, j], dp[i, j-1], dp[i-1, j-1] + 1

Iterative DP - Squared Space

Complexity

time: $O(nm)$ single pass for each matrix element
space: $O(nm)$

def maximalSquare(self, matrix: List[List[str]]) -> int:
    n, m = len(matrix), len(matrix[0])
    dp = [[0 for _ in range(m)] for _ in range(n)]
    res = 0

    for i in range(n):
        for j in range(m):
            if i == 0 or j == 0:
                dp[i][j] = int(matrix[i][j])
            else:
                if matrix[i][j] == '1':
                    dp[i][j] = min(dp[i-1][j], dp[i][j-1], dp[i-1][j-1]) + 1
            res = max(res, dp[i][j])

    return res ** 2

Iterative DP - Linear Space

Since dp only uses one entry from previous iteration: dp[i-1][j-1], we could just use 1D dp array and instead map dp[i-1][j], dp[i][j-1], dp[i-1][j-1] to dp[j], dp[j-1], and prev, respectively.

Complexity

time: $O(nm)$
space: $O(m)$

def maximalSquare(self, matrix: List[List[str]]) -> int:
    n, m = len(matrix), len(matrix[0])
    dp = [0 for _ in range(m)]
    prev = 0
    res = 0

    for i in range(n):
        for j in range(m):
            temp = dp[j]
            if i == 0 or j == 0:
                dp[j] = int(matrix[i][j])
            else:
                if matrix[i][j] == '1':
                    dp[j] = min(dp[j-1], dp[j], prev) + 1
                else:
                    dp[j] = 0
            prev = temp
            res = max(res, dp[j])

    return res ** 2